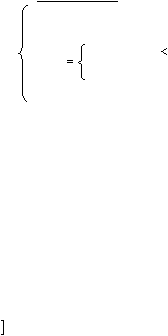
94
Из этой формулы видно, что конечный результат равно как и результат первого присваива-
ния зависит от начального значения mn
0
переменной mn. Однако эта величина не имеет опреде-
ленного значения, соответственнно неопределен и конечный результат выполнения алгоритма в
целом, что и является ошибкой.
В самом деле, если значение mn
0
окажется меньше любого из значений последовательности
х[1], .... x[N], то конечный результат вычислений будет неправильным. В частности, при реализа-
ции алгоритма на Бейсике неправильный результат будет получен, если последовательность будет
состоять только из положительных чисел. Например, для последовательности чисел: 1, 2, 3, ..., N.
Приведем правильную версию алгоритма с доказательством отсутствия ошибок, используя
технику индуктивных утверждений.
алг «нахождение минимума»
массив х[1:п]
нач
тп := x[1]
от k = 1 до N цикл
если x[k] < тп то
тп = x[k]
все
кцикл
Min = тп
кон
Результаты:
mn
0
= х[1]
[k = (1 ... N)]
случае
ином
в
,
mn
mn
x[k]
при
],
k
[
x
mn
1
-
k
1
-
k
k
Min = mn
N
Утверждение. Для любой последовательности чисел x[l:N] конечным результатом вычис-
лений будет значение Min = Min (х[1], ..., x[N]).
Доказательство. Воспользуемся результатами анализа выполнения алгоритма, рассмот-
ренного ранее. Различие между ними состоит в добавлении перед началом цикла присваивания mn
:= х[1], которое задает начальное значение переменной mn, равное mn
0
= х[1].
Тогда в силу приведенных ранее рассуждений и выкладок конечным результатом выполне-
ния новой версии алгоритма будет значение
Min = mn
N
= Min(x[N], x[N-l], ..., х[2], х[1], mn
0
) =
= Min(x[N], x[N-l], ..., x[2
, x[l], x[l]) = Min(x[N], .... х[1]).
Что и требовалось.
Рассмотренные примеры являются образцами доказательств правильности алгоритмов и
программ, которые могут использоваться для анализа и доказательства правильности других но-
вых алгоритмов и программ обработки данных.
Общий вывод, который мы хотим сделать, состоит в том, что применение доказательных
методов превращает программирование в научную дисциплину создания безошибочных алго-
ритмов и надежных программ для ЭВМ.
В о п р о с ы
1. Как показать наличие ошибок в алгоритме?
2. Сколь долго может продолжаться отладка программ?
3. Зачем нужны доказательства в анализе алгоритмов?
4. Из чего состоит техника доказательств правильности?
5. Когда применяется разбор случаев?
6. Что такое леммы?
7. Что такое индуктивные рассуждения?
3 а д а ч и
1. Приведите постановку, алгоритм решения и разбор правильности для следующих задач:
а) подсчет суммы целых чисел;
б) подсчет суммы нечетных чисел;
в) подсчет членов арифметической прогрессии;

