69
Особенностью систематических методов является возможность полного устранения оши-
бок из алгоритмов и программ. При этом подходе программы сверяются с описаниями алгорит-
мов, а алгоритмы - с описаниями сценариев и методов решения.
Такой систематический подход к составлению алгоритмов и программ может применяться
к решению на ЭВМ любых прикладных задач с использованием самых различных языков про-
граммирования - Бейсик, Паскаль, Си и им подобные. Приведем примеры систематического ре-
шения задач.
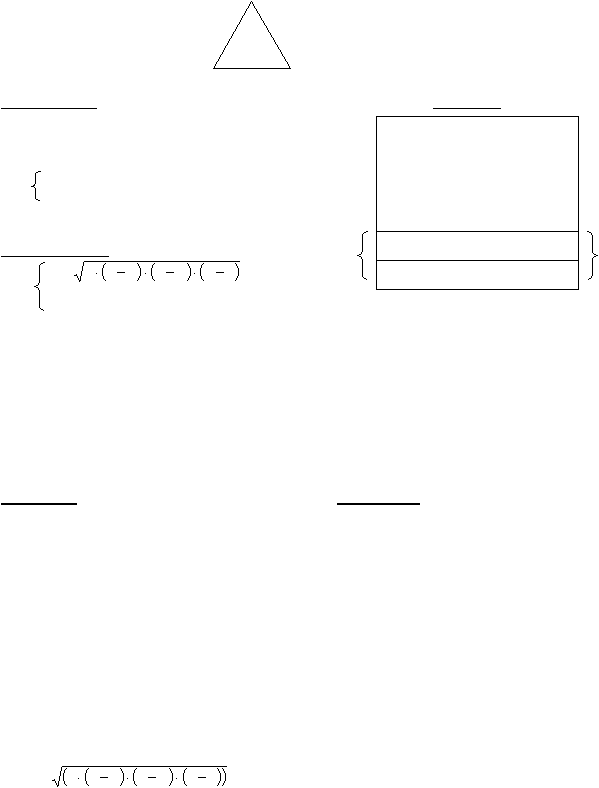
Первая задача: подсчет площади треугольника по длинам сторон.
a b
c
Постановка
Сценарий
Дано: а, b, с - длины сторон,
площадь треугольника
Треб.: S - площадь треугольника,
длины сторон:
При: а > 0, b > 0, с > 0,
а =? <а>
a < b +c, b < a + c, c < a + b.
b =? <b>
с =? <с>
Метод решения
площадь = <S>
S =
c
p
b
p
a
p
p
недопустимы длины
р = (а + b + с)/2
Обратите внимание: в постановке задачи в исходные условия включены ситуации, когда
решение может не существовать. А именно, здесь указаны три неравенства треугольника и усло-
вия положительности длин сторон. При нарушении этих условий треугольника просто не сущест-
вует и тем более нельзя говорить о его площади.
Для надежности программ такого рода ситуации (когда нет решений) должны быть пре-
дусмотрены в сценарии диалога. В этих случаях в сценарий необходимо включить сообщения с
диагностикой причин отказов: отсутствие решений, недопустимость данных, некорректность ко-
манд, противоречивость фактов и т. п.
Алгоритм
Программа
алг «площадь треугольника»
' площадь треугольника
нач
cls
вывод («площадь треугольника»)
? «площадь треугольника»
вывод («длины сторон:»)
? «длины сторон:»
запрос («а=», a)
input «a=», a
запрос («b=», b)
inpnt «b=», b
запрос («с=», с)
input «c=», c
если не (а > 0 и b > 0 и с > 0) то
if a<=0 or b<=0 or c<=0 then
вывод («недопустимы длины»)
? «недопустимы длины»
инеc не (а < b + с и b < а +
elseif not (a < b+ с and b < а + с
+с и с<а+b)то
and с < а + b) then
вывод («недопустимы длины»)
? «недопустимы длины»
иначе
else
р := (а + b + с)/2
р = (а+ b +с)/2
S :=
c
p
b
p
a
p
p
S = sqr (p*(p-a)*(p-b)*(p-c))
вывод («площадь=», S)
? «площадь=», S
все
end if
кон
end

