92
Возвращаясь к исходному уравнению (9.2), заметим, что если x
0
=
k
(т. е. z
0
=k), то задача Коши
имеет решение x(t)
x
0
(рис. 9.1). Если x
0
<
)
(
0
k
z
k
, то уравнение (9.6) интегрируется следующим
образом
ln z – ln(k-z)=ln z
0
-
ln (k-z
0
)+k(t-t
0
),
откуда
)
(t
0
0
0
t
k
e
z
k
z
z
k
z
, (9.7)
значит,
2
)
(t
0
)
(t
0
))
1
(e
(k
)
(t
0
0
t
k
t
k
x
e
kx
x
, t > 0 (9.8)
Если x
0
>
k
, то аналогично предыдущему случаю снова получаем формулу (9.8). Дифференцируя
(9.8) по t, имеем
2
)
(t
0
)
(t
0
0
))
1
(e
(k
)e
(
0
0
t
k
t
k
x
x
k
kx
dt
dx
, (9.9)
откуда вытекает, что при X
0
<
k
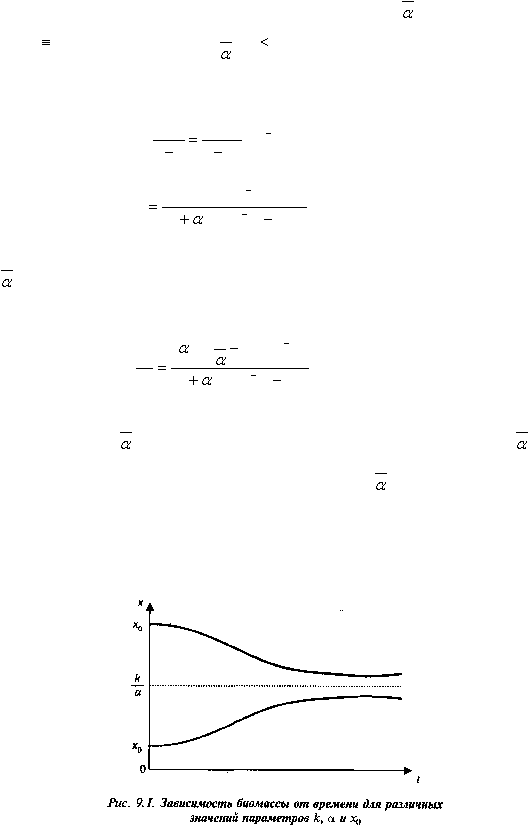
график функции х(t) монотонно возрастает, а при x
0
>
k
– монотонно
убывает, причем оба графика имеют горизонтальную асимптоту х=
k
(рис. 9.1). Мы не приводим здесь
элементарную, но громоздкую формулу второй производной d²x/dt², показывающую, что верхний и
нижний графики имеют по одной точке перегиба.
Мы рассмотрели весьма упрощенную ситуацию, так как предполагали, что популяция не
взаимодействует ни с какими другими популяциями, учет же этого обстоятельства, конечно,
значительно усложняет модель.
Рассмотрим одну из таких моделей. Будем обозначать биомассы двух популяций через х и у
соответственно. Предположим, что обе популяции потребляют один и тот же корм, количество
которого ограничено, и из-за этого находятся в конкурентной борьбе друг с другом.
Французский математик В. Вольтерра в 1926 г. показал, что при таком предположении динамика
популяций достаточно хорошо описывается следующей системой дифференциальных уравнений:

