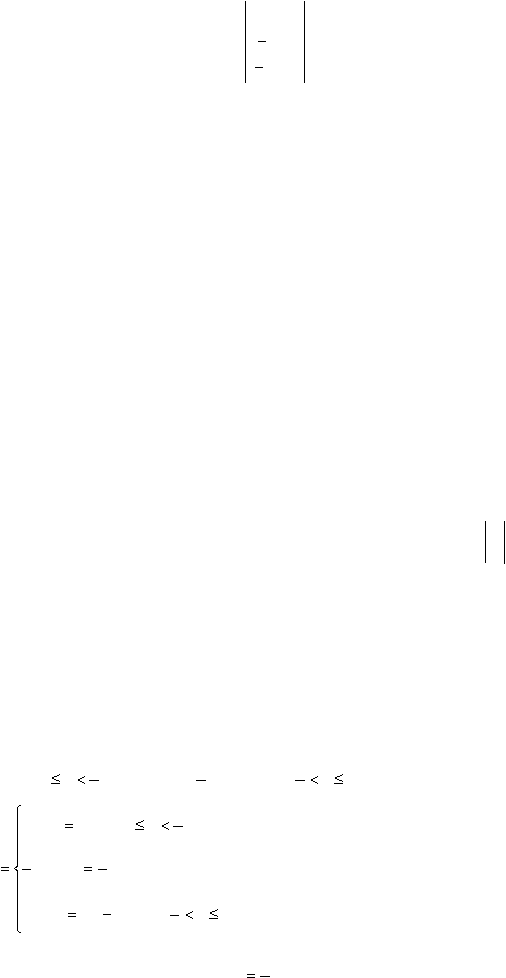
109
B
A0
.
6
3
2
1
7
5
1
9
8
4
5
Эта запись означает, что игрок А выбирает одну из строк этой матрицы, а игрок В, не зная выбора А,
выбирает один из столбцов матрицы. Число на пересечении выбранных строки и столбца определяет
выигрыш первого игрока (соответственно проигрыш второго). Например, если А выбрал вторую строку,
а В – третий столбец, то А выиграл 5 единиц, а В их проиграл. Если же А выбрал третью строку, а В –
второй столбец, то А проиграл 2 единицы, а В их выиграл.
Будем считать, что цель каждого из игроков состоит в максимизации наименьшего возможного
выигрыша (соответственно минимизации наибольшего возможного проигрыша). Основной вопрос,
возникающий в теории игр: существует ли наилучший способ игры у каждого из игроков, т. е. имеются
ли у них оптимальные стратегии.
Прежде чем сформулировать ответ, вернемся к рассматриваемой матрице. Сразу видно, что игроку А
выгоднее всего выбрать первую строку, так как все ее элементы больше соответствующих элементов
остальных строк. Точно так же игроку В выгоднее всего выбрать второй столбец, так как все элементы
этого столбца меньше соответствующих элементов остальных столбцов. Следовательно, в данном
примере оптимальными стратегиями будут следующие: для А – выбор первой строки, а для В – выбор
второго столбца. Число 4, стоящее на пресечении первой строки и второго столбца, носит название
цены игры, т. е. платы, которую получает оптимально играющий игрок. Таким образом, в этом примере
гарантированный выигрыш
А – не менее 4-х единиц и гарантированный проигрыш В – не более 4-х
единиц (он равен 4 единицам, если оба игрока играют оптимально).
Если оказывается, что для данной платежной матрицы минимум в какой-либо строке совпадает с
максимумом в каком-либо столбце, то эти строка и столбец называются оптимальными, а их
пересечение – седловой точкой платежной матрицы. Соответствующее число и будет ценой игры.
Однако далеко не каждая матрица имеет седловую точку, например, матрица
B
A
40
01
седловой точки
не имеет. Говорить здесь о максимизации наименьшего возможного выигрыша (минимизации
наибольшего возможного проигрыша) возможно только при использовании так называемой смешанной
стратегии при многократной игре с одной и той же платежной матрицей. Суть этой стратегии
заключается в выборе разных стратегий с определенными частотами. Итак, пусть А выбирает первую
строку с частотой х, а вторую – с частотой (1 –
х). Аналогично для В соответствующие частоты
обозначим через у и (1 –у). Тогда средний выигрыш А, обозначаемый через Е (х, у), равен
Е(х,у)=4(1-х)у+х(1-у)=х+4у-5ху.
(11.17)
Нас интересует величина max min E(x,y). Имеем
x
y
Е
у
=4-5х,
(11.18)
откуда Е
у
>0 при
5
4
0
x
, E
y
=0 при х=
5
4
и Е
у
<0 при
1
5
4
x
. Значит,
1
5
4
)
1
(
4
)
0
,
(x
,
5
4
5
4
,
5
4
0
)
1
,
(x
)
,
(
min
x
при
x
E
x
при
x
при
x
E
y
x
E
y
(график на рис. 11.7). Следовательно,
5
4
)
,
(
min
max
y
x
E
y
x
(11.19)

