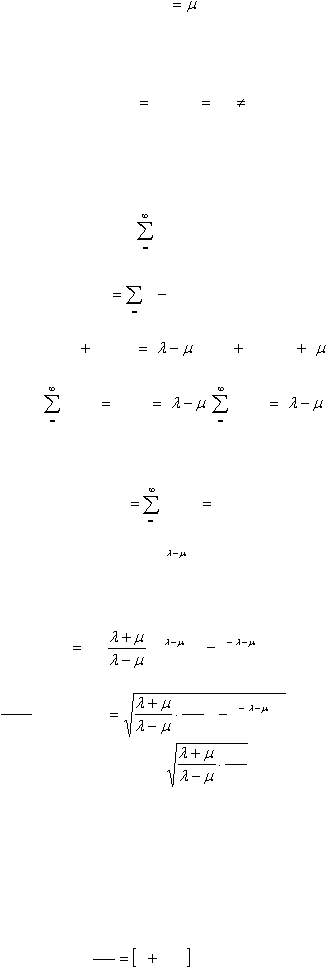
100
).
(t
)
(t
1
'
0
p
p
(10.6)
(естественно считать, p
-1
(t)
?0).
Если в начальный момент времени t=0 в популяции имелось N
0
особей, то начальные условия для
системы обыкновенных дифференциальных уравнений с постоянными коэффициентами (10.4)–(10.6)
имеют вид:
.
,i
0
)
0
(
,
1
)
0
(
0
0
N
p
p
i
N
(10.7)
Рассматриваемый процесс гибели и рождения является случайным процессом (классическим
примером цепей Маркова [17]), а само решение задачи (10.4)–(10.7) можно получить стандартными
методами теории обыкновенных дифференциальных уравнений (см., например, [47]). Нас интересуют
следующие вероятностные характеристики: ожидаемое значение, т. е. среднее значение популяции в
момент времени t
N(t)=
1
i
i
ip
(t)
(10.8)
и вариация (дисперсия), т. е. среднее квадратичное отклонение от N(t)
n
i
i
t)
p
t))
N(
i
N
1
2
(
(
)
var(
. (10.9)
Для вычисления N(t) заметим, что из уравнения (10.5) и первого уравнения из (10.4) вытекает
).
(t
3
))
(t
2
)(
(
)
(t
2
)
(t
3
2
)
(t
1
'
2
'
1
p
p
p
p
p
Продолжая этот процесс сложения, получим
1
'
1
'
),
(t
)N
(
)
(t
)
(
)
(t
)
(t
i
i
i
i
ip
N
ip
т. е. обыкновенное дифференциальное уравнение
N'(t)=(? - ?)N(t) (10.10)
с начальным условием (10.7)
p
i
i
N
ip
N
.
)
0
(
)
0
(
0
(10.11)
Решение его, очевидно, равно
N(t)=
t
e
N
)
(
0
, (10.12)
в частности, при ? > ? численность популяции экспоненциально возрастет (при ?=?+a определяется
уравнением (10.3)), а при ? < ? экспоненциально убывает при t
> ?.
Аналогично (см. [17]) вычисляется
вариация
),
1
(
)
var(
)t
(
)t
(
2
0
e
e
N
N
(10.13)
откуда при ? > ? для коэффициента вариации получаем выражение
),
1
(
1
))¹
(var(
)
(t
1
)t
(
0
2
/
e
N
N
N
(10.14)
которое при t
> ?
с
тремится к величине
0
1
N
. Следовательно, при достаточно больших
начальных значениях популяции N
0
среднее квадратичное отклонение от N(t) является равномерно
малым, и детерминистская модель дает адекватное представление о поведении популяции при больших
значениях времени.
10.2. Случайные изменения среды
Рассмотрим теперь модель, учитывающую случайные изменения среды. Простейшая модель,
соответствующая уравнению (10.1), имеет вид
,
)
(t
N
y
a
dt
dN
(10.15)
N(0)=N
0
,
(10.16)

