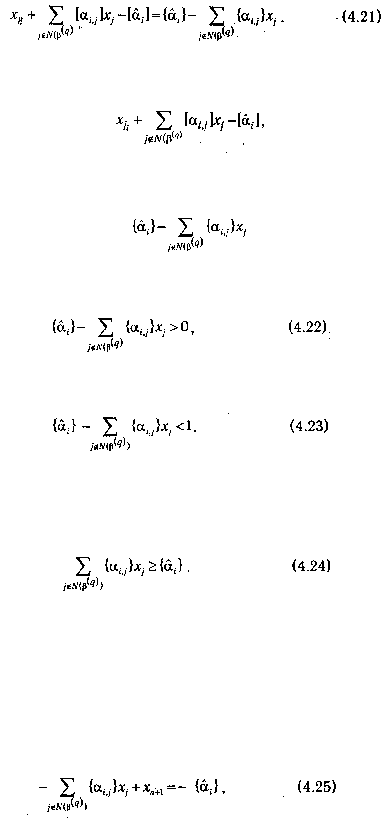
80
или
Из (4.21) следует, что если все х
j
,
j?1: n являются целыми, то целым будет и выражение
стоящее в левой части (4.21), и, стало быть, правая часть данного уравнения:
также должна быть целой. Предположим, что
тогда, в силу того, что 0
? {
?
i
} < 1, а {
?
i,j
}
? 0,
x
j
? 0,
должно вы
полняться неравенство
Однако неравенства (4.22) и (4.23) противоречат требуемой целочисленности правой части (4.21)
x
j
(?
(q)
). Следовательно, для целочисленных решений должно выполняться условие, противоположное
неравенству (4.22), или, что то же самое,
В то же время (4.24) не выполняется для любого нецелочисленного базисного плана х.
Действительно, небазисные компоненты плана равны нулю: х
j
=0 , j?N(?
(q)
), и (4.24) приобретает вид
{?
i
}
?
0 <=> {?
i
}
=0, но это противоречит предположению о нецелочисленности плана х, т. к. в базисном
плане х
i
= ?
i
. Все сказанное позволяет утверждать, что ограничение (4.24) задает правильное отсечение.
Таким образом, с точки зрения организации техники, вычислений для осуществления правильного
отсечения мы должны к системе ограничений нецелочисленной линейной задачи, решаемой на q-й
итерации, добавить условие
где x
n+1
?0
— фиктивная переменная, добавляемая для преобразования неравенства в строгое равенство.
Ей соответствует нулевой коэффициент в целевой функции.
Данному преобразованию условий задачи будет соответствовать преобразование симплекс-таблицы,
показанное на рис. 4.2. На нем по соображениям обеспечения наглядности использованы обозначения
(4.17) и предполагается, что текущий базис
?
(q)
состоит из первых m столбцов.

