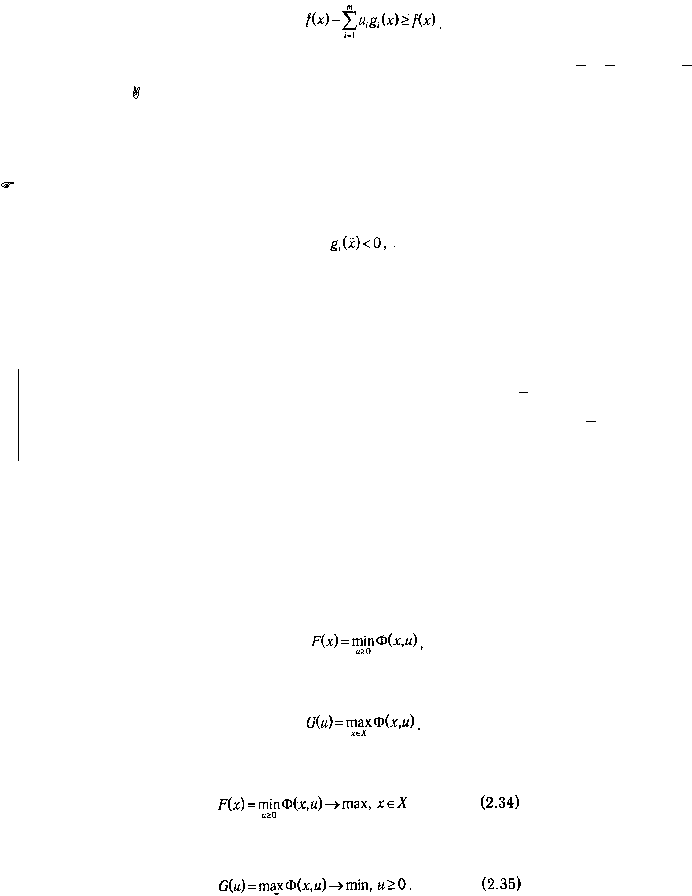
58
Значит,
Окончательно получаем, что для любых х?D справедливо соотношение f(x)?f(x), т. е. х — оптимальный
план задачи (2.28).
Утверждение, обратное теореме (2.3), т. е. необходимое условие экстремума в ЗНП, оказывается
верным только при выполнении дополнительных условий, которым должна удовлетворять задача (2.28).
Важнейшим из них является так называемое условие регулярности Слейтера:
Говорят, что функция g
i
(х), задающая ограничение в задаче (2.28), удовлетворяет условию
регулярности Слейтера, если существует такая точка
x
~
, принадлежащая области
допустимых планов D, что
т. е.
x
~
является внутренней точкой относительно ограничения
g
i
(x).
Поэтому данное условие также
называют условием телесности.
Вообще говоря, существуют разные варианты необходимого условия Куна—Таккера. Приведем один
из них.
Теорема 2.4. (Необходимое условие наличия экстремума).
Если (D, f) является задачей выпуклого программирования с решением х, ее целевая функция f(x) и
функции ограничений g
i
(x) — дифференцируемы, нелинейные ограничения в форме неравенств
удовлетворяют условию регулярности Слейтера, то существует такой вектор и ? 0, что (х,и) —
седловая точка функции Лагранжа Ф(х,и).
Мы не будем здесь приводить доказательство теоремы (2.4), которое является довольно сложным.
Заинтересованный читатель может найти его в таких источниках, как [1, 13].
Значение теоремы Куна—Таккера состоит в том, что она позволяет связать процесс решения
оптимизационной задачи с поиском седловых точек функции Лагранжа, т. е., грубо говоря, с
максимизацией этой функции по х и минимизацией по и.
Определим F(x) как функцию, ставящую в соответствие каждому значению х минимальное значение
функции Ф(х,и) по и:
и по аналогии
Рассмотрим задачу отыскания максимума функции F(x)
и задачу минимизации G(u)
Очевидно, что

